德州扑克AI算法浅析

不完全信息的博弈是一种玩家对正在玩的游戏没有共同知识的博弈，也就是说，不能只通过子游戏的信息解决子游戏，这样通常达不到全局最优。在相关研究中，通常的做法是逼近游戏中的纳什均衡策略，也就是每个玩家都无法通过只改变自己的策略来提高自己的收益。在零和游戏中，如果每个玩家都选择对对手的最优策略，那么游戏整体就达到了纳什均衡，每个玩家的策略就是最优策略（纳什均衡策略）。

这几年有明显突破的领域是双人不限注德州扑克，阿尔伯塔大学的DeepStack和CMU的Libratus都取得了明显的突破，尤其是Libratus，已经完胜了顶级人类玩家和其他AI。顺便说一下，限注的德州扑克的决策点的数量是\(10^{14}\)，已经可以被完全搜索；不限注的德扑的决策点数量是\(10^{161}\)，和围棋的\(10^{170}\)很接近。而在其他领域，尤其是多人游戏，如麻将（\(10^{150}\)），AI还没有显著成果。这篇文章主要介绍DeepStack和Libratus的算法。

DeepStack

论文：DeepStack: Expert-Level Artificial Intelligence in Heads-Up No-Limit Poker

同样的，DeepStack的目标也是逼近纳什均衡策略，而纳什均衡本身就是最优策略，文章原文：

In two-player zero-sum games, like HUNL, a solution or Nash equilibrium strategy maximizes the expected utility when playing against a bestresponse opponent strategy.

在解释具体算法之前，首先介绍一下文章里的一些术语和定义：

range：指根据公共牌和玩家历史操作得出的玩家持有各种手牌的概率，具体来说，德州扑克每位玩家有两张底牌，排列组合的所有可能性为\((52\times51)/2=1326\)种，所以range是一个长度为1326的vector，里面的值就是相应手牌的概率。
utility：在游戏终止状态下根据游戏规则计算的效用（奖励）。
expected utility：在非终止状态下达到各种终止状态的期望效用。
best-response strategy：根据对手的策略能最大化自己的期望效用的策略。
public state：由公开信息组成的状态，如公共牌，下注历史等。
information set (infoset)：infoset里包含许多state，但是根据玩家已知的信息无法区分它们的区别
counterfactual value: 其实就是期望效用，原文：

Each value in the opponent’s vector is a counterfactual value, a conditional “what-if” value that gives the expected value if the opponent reaches the public state with a particular hand.

DeepStack的核心算法叫Continual Re-solving，就是反复遍历搜索树，并用Counterfactual Regret Minization (CFR)算法持续优化策略，并结合value network对超过指定深度的节点进行评估。它的部分搜索树如下图所示。

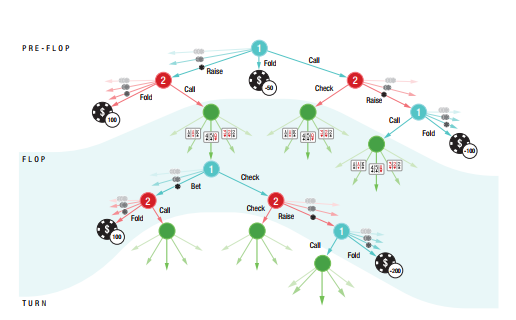
具体来说，DeepStack并不保存以前的策略，每次需要行动时即时计算策略。对于在任意public state计算相应策略，只需要提供自己的range和对手的counterfactual values即可，也就是说，这些信息就足以总结当前状态下所有对玩家可知的信息。注意，这里的counterfactual values不是一个值，而是一系列值，对应对方的每种手牌，也就是说，它是一个长度为1326的vector。为了能够即时计算策略，我们需要从游戏的开始追踪自己的range和对手的counterfactual values，在游戏的开始，range被初始化为uniform distribution，而counterfactual values被初始化为每种底牌的value。在游戏进行中，需要不断更新它们的值：

自己行动时：根据计算好的策略更新counterfactual values；根据策略和贝叶斯定律更新range
翻公共牌时：根据上次的策略更新counterfactual values；如果翻牌出现四张同样的牌，则需要把range里出现相应牌的概率置0。
对手行动时：不需要更新。

文章里说这样的更新就能够满足条件，并应用下面的搜索算法能够保证收敛到近似的纳什均衡。

下面来看算法的具体步骤，其中S代表public state，r代表range，v代表counterfactual value，I代表Information set，\(\sigma\)代表策略，R代表后悔值（后面会讲什么含义）：

算法的输入为public state, 自己的range，对手的counterfactual value，和infoset。首先随机初始化一个策略和对手的range，然后初始化regret为0。初始化完成之后进入循环搜索的过程，在每次搜索传入当前策略和双方range计算出双方的counterfactual values，然后根据此值来改进策略和更新对手的range，再用改进后的值进行下一次搜索，直到循环次数达到要求。循环完毕后取平均策略最为这次行动的最终策略，然后据此sample一个action，更新range和对手的counterfactual value，re-solve的过程就结束了。

具体来看搜索过程，搜索是基于深度优先搜索，并且限制深度，如果限制深度为4的话，复杂度可以降到\(10^{17}\)，DeepStack还进一步应用了action abstraction，即只考虑部分action，复杂度进一步降到了\(10^7\)。搜索算法如下：

首先判断S是不是终止状态，如果是的话就根据utility更新counterfactual values；再判断达没达到最大搜索深度，达到的话就交给神经网络来评估；如果都符合条件的话就继续进行搜索，遍历当前状态下所有action（限制后的），到达下一个状态，更新r和v，递归搜索下去。最后返回双方的counterfactual values。

CFR

评估完counterfactual values之后需要计算当前的策略，使用的算法是CFR。它定义了一个regret值，其含义是在当前状态下，我选择行为A而不是行为B的后悔程度。比如，在石头剪刀布中，对方出了剪刀，我出了布，这个时候，我会更后悔没有出石头，相比之下不那么后悔没出剪刀。

一个regret的定义是后悔没选的action达到的state的counterfactual value与当前状态的counterfactual value的差值。比如在上面的例子中，在对方出剪刀的情况下，我出布的utility (counterfactual value)是-1；出剪刀的utility是0；出石头的utility是1。因此我选择布而不是剪刀的后悔值R（剪刀->布）= 1；而不选择石头的后悔值R(石头->布）= 2。

定义了后悔值之后，我们可以应用Regret Matching的方法来进行决策，其思路是倾向于选择后悔值更大的行为。比如，在石头剪刀布中，如果我们进行了n次游戏，然后把每次游戏所有action的后悔值加起来，然后做一个归一化，就可以得到一个概率分布作为我们的策略： \[ R(a)=\sum_{i=1}^nR_i(a_i) \]

\[ P(a)=\frac{R(a)}{R(剪刀)+R(石头)+R(布)} \]

而在每一步的后悔值由对手的行为所决定，所以CFR算法其实是在根据对手的策略改变我们自己的策略。DeepStack中的实现如下：

下面那个函数是根据Regret更新对手的range，应该是CFR算法的变种，这里就不具体介绍了。

神经网络

最后来看神经网络部分，网络的输入为双方的range, pot size和公共牌信息，输出为评估的双方的counterfactual values，网络的结构是7个全连接层，由于是零和游戏，最后的value需要做归一化处理。除此之外，在输入到神经网络前要做个预处理，把range聚类为1000个bucket，最后再把输出的counterfactual values映射回去，如下图所示。

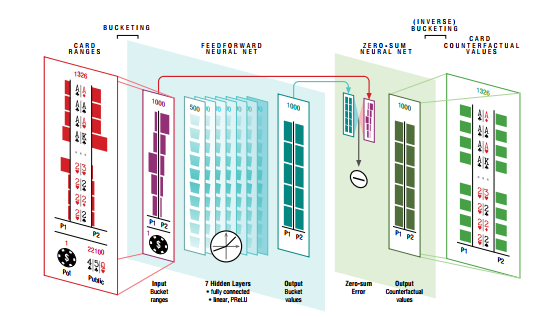
这样的网络有两个，一个用来评估转牌局的value，叫转牌网络；另一个用来评估翻牌局的value，叫翻牌网络。网络的训练方式很特别，既不是使用人类玩家的数据也不是自我博弈，而是用随机生成的数据！首先，随机生成1千万个转牌局面：range, public cards, pot size都是随机生成的，作为转牌网络的训练数据，然后通过求解限制action的子游戏生成网络的target，解法就是之前的搜索算法，为什么可以解？因为一方面限制了action的选择，另一方面这是德扑的倒数第二轮，在4张公共牌确定的情况下搜索空间已经不大了，所以可以直接求解出counterfactual value。训练翻牌网络同样是用随机生成的数据，target是用上面的depth-limit solving procedure和转牌网络生成。

实力

尽管论文里说DeepStack是第一个战胜人类顶级玩家的AI，但实际上和它比赛的对手都不是顶级玩家，只能算是高手，而且有些高手赢得也并不轻松。另一方面，DeepStack也没有提高和之前AI的比赛数据，所以它的实力恐怕没有说的那么高，我认为用随机生成的数据来训练可能是它的瓶颈。下图是它的竞争对手Libratus的作者给出的，可参考性较高。

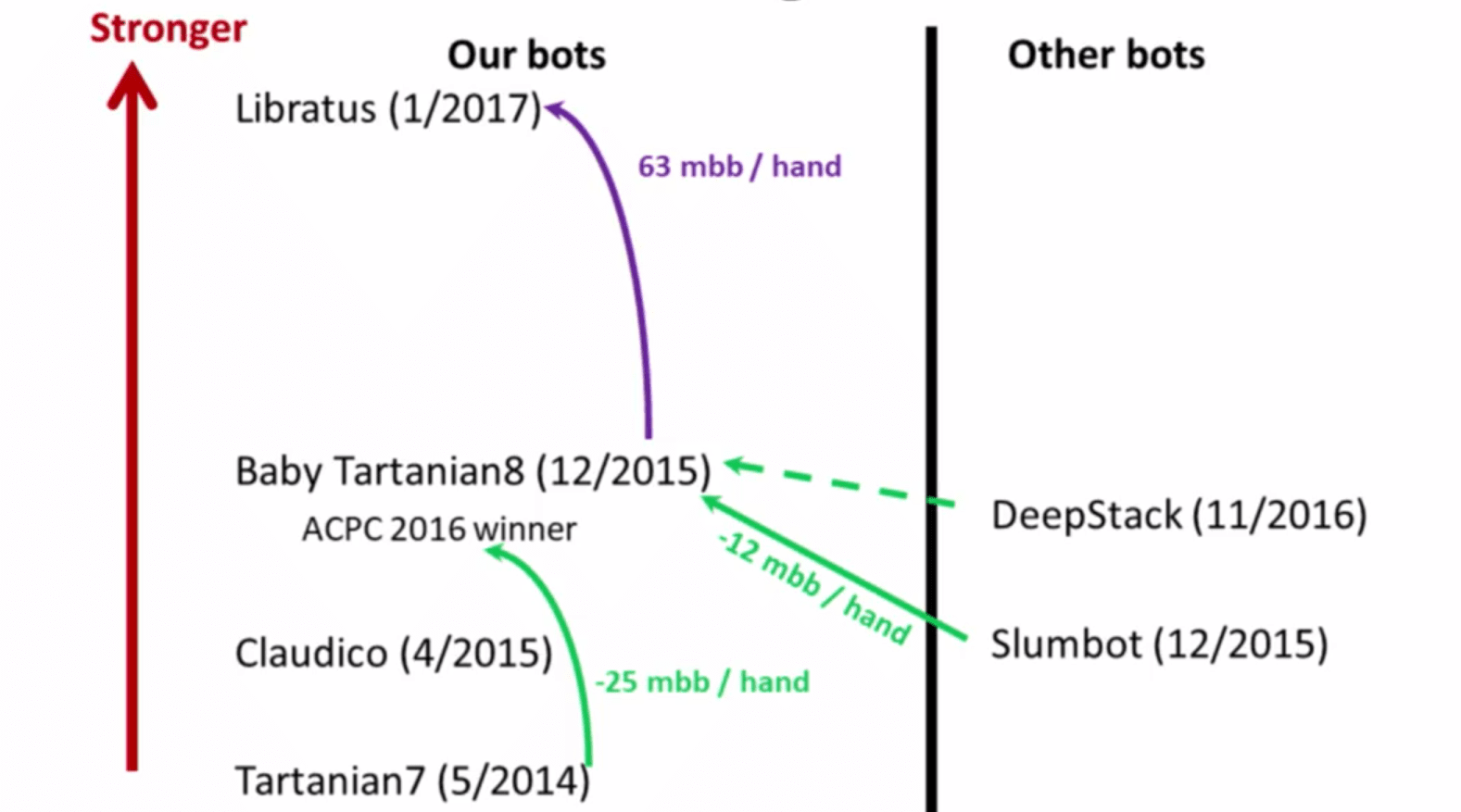
总结

优点：CFR搜索+Value net的结构不错，感觉可以应用到其他不完全信息博弈的游戏中；另外DeepStack的理论基础也比较完备，能够保证收敛到近似纳什均衡。

不足之处：实力差强人意，根据给出的数据只能说是人类高手水平，未必能击败顶级选手；训练数据随机生成可能是实力的瓶颈，而且这点难以应用到其他游戏中，计算量也不小。

Libratus

论文

Libratus由三部分组成，分别是蓝图策略，子游戏求解和自我增强模块。蓝图策略是赛前计算的宏观策略，由于德扑复杂度很高，计算时进行了一些抽象；子游戏求解是在游戏进行时对根据蓝图策略和已知信息对子游戏进行即时求解，得到更好的策略；自我增强模块是指把实际对战中遇到的蓝图里没有的分支加到蓝图里。

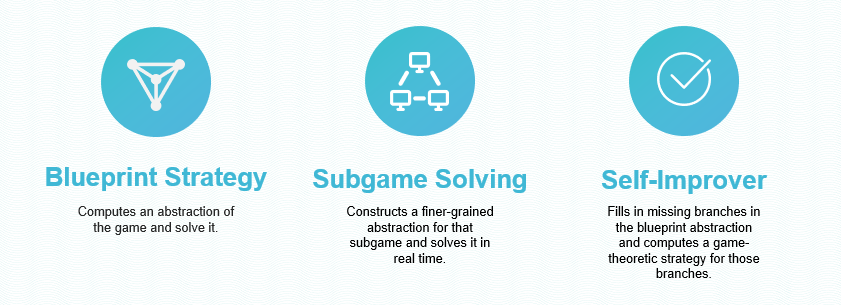
Blueprint Strategy

直接计算整体策略复杂度太高，所以需要对游戏进行抽象。抽象分为两个方面，分别是行为抽象（Action Abstraction）和卡牌抽象（Card Abstraction）。行为抽象是指不考虑所有可能的下注，即从100到20000的任意整数，只考虑以100为增量的下注，即100，200，300....。这样抽象可以大大减少决策树的宽度，而且下100和101区别也不大。卡牌抽象是指对同类型的卡牌进行聚类，像KKK和QQQ区别也不是很大，这里主要指的是公共牌。Libratus在第三轮和第四轮的时候对公共牌进行了聚类，第三层把5500万的可能性减小到250万，第四层把24亿的可能性减小到125万。

计算蓝图策略的算法是External-Sampling Monte Carlo Counterfactual Regret Minimization (ES-MCCFR)，看着名字很长，其实就是Monte Carlo模拟+CFR，即搜索时用CFR计算的策略，搜索完毕用action的访问计数来计算策略。

算法需要对每个infoset \(I_i\)的每个action \(a\)维护两个值，分别是regret \(R(I_i,a)\)和访问计数\(\phi(I_i, a)\)，搜索完毕后根据\(\phi(I_i,a)\)的分布行动。搜索算法和DeepStack的continual re-solve很像，也是重复搜索T次，每次搜索时确定一个正在搜索的玩家\(P_i\)，其他玩家记为\(P_{-i}\)，算法如下，其中\(h\)为state：

注意到，对于\(P_i\)的state，搜索其中所有action；而对于\(P_{-1}\)的state，只根据CFR sample出一个action，并增加其访问计数。还有一个对应的函数叫TRAVERSE-ESMCCFR-P，是加了剪枝的版本，这里就不列出了，有兴趣的同学可以找论文查看。

最后计算策略也是用CFR算法：

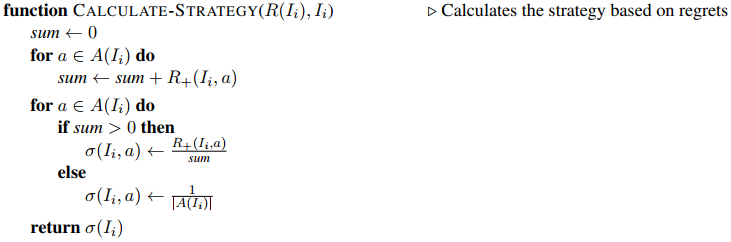
Subgame Solving

由于蓝图策略在第三轮和第四轮进行了比较严重的抽象，在实际比赛时需要重新计算更合适的策略，也就是subgame solving了。解子游戏和计算蓝图策略的算法是一样的，区别在于这时子游戏可以得知更多的信息，如public card、对手的历史操作等，所以计算出的解通常优于蓝图策略。为了确保子游戏策略不比蓝图策略差，还在最后引入了蓝图策略的分支，如果子策略不好的话，算法可以直接选择原策略，如下图所示：

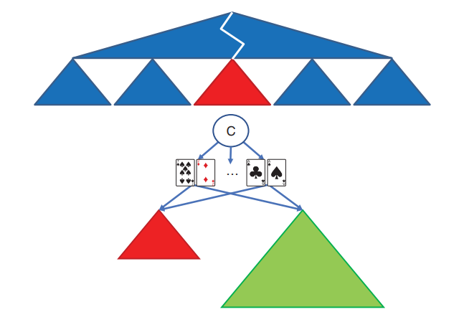
Self-Improver

自我强化模块，这个是指在实际比赛中会遇到蓝图策略中没有的分支，赛后把它加在蓝图策略上，这样就能随着比赛的增多越来越强。

总结

优点：理论完备，文章证明该方法可以收敛到纳什均衡；实力超群，唯一一个能击败顶级人类玩家的德州扑克AI。

缺点：计算量太大，Libratus运行在超算中心上，需要200~600个节点，每个节点14核128G内存，共计算了12 million core time...